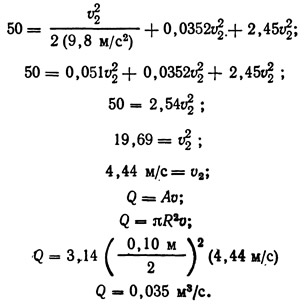Режим движения
Режим движения жидкостей может быть ламинарным и турбулентным. Если представить жидкость как тело, состоящее из отдельных частиц или элементов, то ламинарный режим движения можно определить как движение, при котором все частицы тела движутся в одном направлении с одинаковой скоростью. Таким образом, частицы образуют струйки (или слои), движение которых относительно друг друга постоянно и завихрения отсутствуют.
Турбулентное движение характеризуется поперечным перемещением струй, завихрениями и другими хаотичными движениями. Потери энергии в турбулентном потоке больше, чем в ламинарном, из-за значительного внутреннего трения.) Для ламинарных потоков благоприятны низкие скорости потоков, трубопроводы небольшого диаметра и высокие вязкости жидкости. Для турбулентного режима благоприятны) противоположные условия. На предприятиях по разведению водных организмов, как правило, имеют дело с турбулентными потоками, так как при высоких ско-ростях1 движения жидкости стоимость эксплуатации трубопроводов уменьшается.
Закон сохранения масс
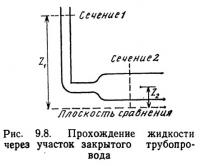
В замкнутом трубопроводе количество жидкости, протекающее через все его сечения, постоянно. На рис. 9.8 изображен участок замкнутого трубопровода, по длине которого взято два сечения — 1 и 2.
Поскольку через оба сечения должно пройти одинаковое количество воды, для этой системы на основе закона сохранения масс можно записать следующее уравнение:
где v — скорость; А — площадь поперечного сечения; γ — удельный вес жидкости.
Учитывая несжимаемость жидкости, проходящей через сечения 1 и 2, можно принять, что
Тогда уравнение (9.23) принимает вид
Уравнение (9.25) называется уравнением неразрывности и является одним из основных уравнений гидродинамики. Полученное Для движения несжимаемой жидкости по замкнутому трубопроводу уравнение (9.25) распространяется также, на движение несжимаемой жидкости в открытом канале.
Пример 9.4. Определить скорость потока в сечении 2 (см. рис. 9.8), если в сечении 1 она составляет 0,5 м/с, а диаметр трубопровода в сечении 2 равен 30 см.
где Q1 — объем жидкости, протекающей в единицу времени через сечение 1.
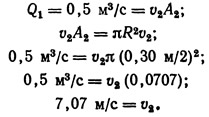
Закон сохранения энергии
Из закона сохранения энергии вытекает еще одно уравнение гидродинамики, позволяющее решать различные задачи. Энергия, которой обладает частица жидкости в любой точке, состоит из потенциальной энергии положения, потенциальной энергии давления и кинетической энергии движения.
Частица жидкости в сечении 1 (см. рис. 9.8) обладает потенциальной энергией, обусловленной ее положением относительно плоскости сравнения или плоскости нулевого энергетического потенциала. Эту энергию (РЕ) е можно выразить как произведение веса частицы W на ее геометрическую высоту над плоскостью сравнения Z1:
Аналогично для частицы в сечение 2 (см. рис. 9.8) можно записать
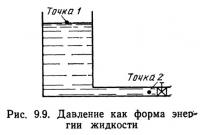
Если жидкость находится под давлением, она обладает потенциальной энергией давления. На рис. 9.9 показан резервуар, заполненный жидкостью, нижняя часть которого переходит в горизонтальный трубопровод. На конце трубопровода установлен клапан, предотвращающий свободное вытекание жидкости из резервуара. Потенциальная энергия частицы в точке 1 (см. рис. 9.9) определяется только ее геометрической высотой, так как единственное давление, оказываемое на поверхность жидкости в! этой точке,— это атмосферное давление, величина которого совпадает с нулевым значением на манометрической шкале отсчета. При закрытом клапане на трубопроводе давление в точке 2 согласно уравнению (9.7) будет равно γh (h — высота заполнения резервуара жидкостью). Это давление способно производить работу, поэтому его можно рассматривать как одну из форм потенциальной энергии. Энергия давления (РЕ)р может быть выражена как произведение веса элементарной частицы жидкости на приложенное к ней давление. В соответствии с уравнением (9.7) давление жидкости можно определить по формуле
отсюда
Движущиеся жидкости обладают кинетической энергией, которую можно определить из основного уравнения
где m — масса; v — скорость.
В соответствии с законами Ньютона
Подставляя формулу (9.30) в уравнение (9.29), получим
Уравнение (9.31) характеризует кинетическую энергию частицы жидкости, движущейся со скоростью V.
Полная энергия частицы жидкости Ее является сумммой потенциальной и кинетической энергии. На основании уравнений (9.26). (9.28) и (9.31) можно получить следующее математическое выражение для величины полной энергии:
В соответствии с законом сохранения энергии полная энергия частицы жидкости в точке 1 должна быть равна полной энергии частицы жидкости в точке 2 (см. рис. 9.9):
Разделив левую и правую части последнего уравнения на W, получим
Уравнение (9.34), известное как уравнение Бернулли, применимо к идеальной жидкости, не имеющей энергетических потерь на участке между сечениями 1 и 2.
В реальных жидкостях всегда имеются потери на трение жидкости о стенки трубопроводов. С учетом этих потерь уравнение Бернулли должно быть переписано следующим образом:
Из уравнения (9.35) видно, что подводимая энергия (например, от насоса, расположенного между точками 1 и 2) должна входить в левую часть уравнения как положительная величина. Потери, обусловленные гидравлическими сопротивлениями, и потери на трение жидкости о стенки трубопровода должны фигурировать в правой части уравнения, относящейся к частице жидкости, расположенной в нижнем по направлению движения жидкости сечении трубопровода, так как они выражают энергетические потери на преодоление сопротивлений трения при движении жидкости от точки 1 до точки 2.
Потери, связанные с преодолением местных гидравлических сопротивлений, возникают при изменении размера поперечного сечения в направлении потока, входе и выходе жидкости и вследствие других изменений Величина таких потерь определяется экспериментально и учитывается при расчетах коэффициентом потерь K, умноженным на скоростной напор:
Полученные экспериментально коэффициенты потерь для трубопроводов приведены в табл. 9.2.
Если на рассматриваемом участке между двумя сечениями трубопровода системы имеется два или более гидравлических сопротивления, потери на их преодоление суммируются.
Пример 9.5. Определить потерю напора в колене трубопровода, изогнутого под углом 90°, с номинальным диаметром, равным 2,54 см, если расход жидкости через это колено составляет 60 л/мин.
Внутренний диаметр трубы с номинальным диаметром 2,54 см равен 2,43 см.
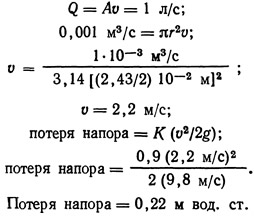
Потери на трение, обусловленные трением жидкости о стенки трубопровода, зависят от скорости движения жидкости, ее плотности, вязкости, диаметра трубопровода и характера шероховатости его стенок. Математически это выражается следующим образом:
где f1 — коэффициент сопротивления трения; v — скорость потока; D — диаметр трубопровода; ε — шероховатость стенок трубопровода (абсолютная); ρ — плотность жидкости; μ — вязкость жидкости; f — функция.
Пять членов этой формулы можно представить в виде двух безразмерных величин:
Одна из этих безразмерных величин ρυD/μ известна как число Рейнольдса (которое может быть выражено так же как υD/v, где v — кинематическая вязкость); другая называется относительной шероховатостью. Можно рассматривать число Рейнольдса как отношение сил инерции к силам вязкости. Число Рейнольдса определяет режим движения потока (ламинарный или турбулентный). Если Re>2000, режим ламинарный, при Re>4000 режим становится турбулентным. В диапазоне чисел Рейнольдса от 2000 до 4000 режим движения потока нестабильный (неустановившееся течение). Потоки, характеризующиеся числами Рейнольдса в этом диапазоне, считаются неблагоприятными в инженерной практике и их следует по возможности избегать.
Вторая безразмерная величина в уравнении (9.37) — ε/D — это относительная шероховатость. Она представляет собой отношение высоты выступов шероховатости на внутренней поверхности трубы к диаметру трубы. Коэффициент сопротивления трения ff также является безразмерной величиной.
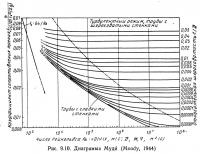
Экспериментальные работы Муди по определению значений безразмерных членов уравнения (9.38) позволили представить зависимость между этими величинами в виде диаграммы, известной теперь как диаграмма Муди (рис. 9.10). По горизонтальной оси диаграммы Муди отложены числа Рейнольдса, по вертикальной — коэффициент сопротивления трения, значения относительной шероховатости представлены отдельной кривой. В ламинарном режиме (Re<2000) коэффициент сопротивления трения является линейной функцией числа Рейнольдса:
где Re — число Рейнольдса.
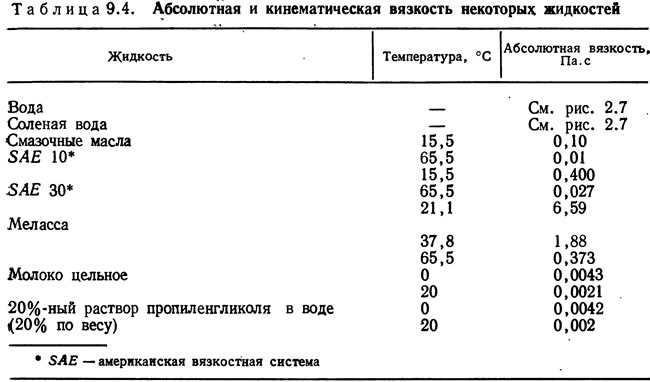
В критическом диапазоне чисел Рейнольдса между значениями 2000 и 4000 точное определение коэффициента сопротивления трения связано с большими трудностями, так как для этого диапазона характерна неустойчивость движения потока, режим которого может все время изменяться от ламинарного к турбулентному и наоборот. При Re>4000 имеет место турбулентное движение, в этом режиме зависимость между числом Рейнольдса и коэффициентом сопротивления трения носит нелинейный характер. Коэффициент шероховатости зависит от материала стенки (табл. 9.3). Для определения числа Рейнольдса можно воспользоваться данными, приведенными в табл. 9.4.
Определив коэффициент сопротивления трения, можно подсчитать потерю напора на преодоление местных сопротивлений:
где h — потеря напора, связанная с местными сопротивлениями, м; ff — коэффициент сопротивления трения (безразмерная величина); L — длина трубопровода, м; D — диаметр трубопровода, м; v — скорость потока, м/с; g — ускорение силы тяжести, м/с2.
Пример 9.6. Определить потерю напора в оцинкованном трубопроводе длиной 100 м с номинальным диаметром 7,62 см, по которому перепускается вода температурой 20 °С. Расход воды составляет 0,06 м/мин.
Внутренний диаметр трубы с номинальным диаметром 7,62 см равен 7,37 см по американским стандартам на трубопроводы.
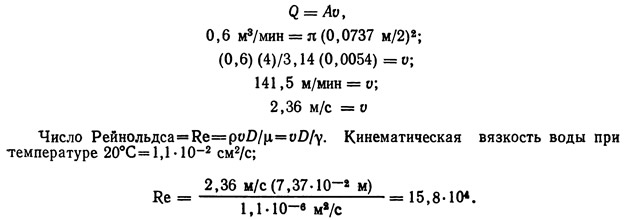
Абсолютная шероховатость оцинкованной трубы по табл. 9.3. равна 0,015 см. Отношение абсолютной шероховатости к диаметру трубы дает относительную шероховатость, в этом примере она равна 0,002. По диаграмме Муди коэффициент сопротивления трения
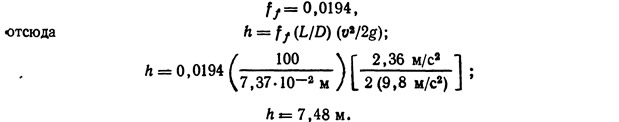
Подводимая энергия на участке трубы между двумя сечениями 1 и 2 [уравнение (9.35)] — это энергия, обычно обеспечиваемая насосом. Необходимо уточнить и конкретизировать эту величину, чтобы получить для нее математическое выражение. Сообщаемую насосом энергию Ер можно представить как произведение веса жидкости W на полный напор системы hp, который должен преодолевать этот насос [уравнение (9.38)];
Вводя это выражение в левую часть уравнения (9.33) вместо величина напора hp, создаваемая насосом, и будет характеризовать величину подводимой энергии в уравнении (9.35).
Теперь уравнение (9.35) можно записать с учетом формул (9.36), (9.40) и (9.41):
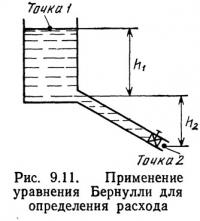
Пример 9.7. Определить расход через оцинкованный трубопровод (рис. 9.11) диаметром 10 см и длиной 200 м; h1=20 м, h2=30 м. В начале трубы расположена полностью открытая задвижка. Число Рейнольдса для трубы равно 1·105.
Для двух сечений, взятых по длине трубопровода 1 и 2, может быть записано уравнение Бернулли. Выбор этих сечений обусловлен соображениями удобства: скорость течения жидкости в сечении 1 может быть принята равной нулю, если учесть, что вместимость резервуара достаточно велика, чтобы движением жидкости в этом сечении 1 можно было пренебречь. Поскольку оба сечения 1 и 2 соединены с атмосферой, манометрическое давление, оказываемое на жидкость в этих сечениях, равно нулю. Уравнение Бернулли будет иметь вид
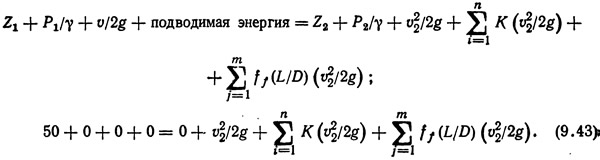
Отдельно для каждого гидравлического сопротивления необходимо определить потерю напора: hfit = потеря напора на входе (кромка прямоугольной формы) + потеря напора в задвижке;
Из табл. 9.2 берут значения:
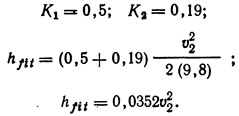
Потеря напора, вызванная трением жидкости о стенки трубы,
Коэффициент сопротивления трения берется по диаграмме Муди.
Число Рейнольдса задано, оно равно 1·105.
Относительная шероховатость оцинкованной трубы составит
От точки 1·105 на горизонтальной оси диаграммы Муди следует восстановить перпендикуляр до пересечения с кривой относительной шероховатости,, соответствующей значению 0,0015, и, следя по горизонтальной оси, найти значение коэффициента сопротивления трения, которое будет равно примерно 0,024.
С помощью уравнения (9.40) можно определить
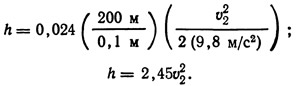
Подстановка полученных значений в уравнение (9.43) дает выражение для расхода:
