Теоретическое решение задачи о такого рода режиме движения до некоторой степени ограниченно. Математически можно показать, что формула (9.44) справедлива для случая движения жидкости в открытых каналах:
где v — скорость потока; С — константа (опытная); R — гидравлический радиус (определение дано ниже); S — уклон канала; х и у — показатели степени (константы) .
Поперечное сечение открытого канала, показанного на рис. 9.12, имеет прямоугольную форму. Глубина канала h, ширина Ь. Таким образом, площадь живого сечения потока
Часть периметра сечения канала, которая соприкасается с водой, называется смоченным периметром
Гидравлическим радиусом называют отношение площади живого сечения к смоченному периметру:
Так, для прямоугольного сечения, показанного на рис. 9.12,
Уклон S в уравнении (9.44) — это уклон дна канала в сторону движения потока, определяемый как перепад высот канала, отнесенный к единице его длины.
Хотя уравнение (9.44) опирается на солидную теоретическую базу, его практическое применение без знания коэффициента С и констант х и у затруднительно. Различные исследователи определяли эти величины эмпирически. Наибольшее распространение получила формула Маннинга, на основе которой построено дальнейшее изложение. Эта формула, называемая формулой Маннинга, была впервые выведена в 1890 г. и записывается в единицах системы СИ в следующем виде:
Полученные экспериментально значения коэффициента n для наиболее распространенных материалов и видов труб приведены в табл. 9.5. Минимальное значение n соответствует условиям движения жидкости в совершенно новых и чистых трубах или каналах; для труб, бывших в употреблении или открытых каналов, забитых растительностью и другими загрязнениями, значения n будут максимальными. При расчете труб и каналов обычно берут средние значения из соответствующего диапазона.

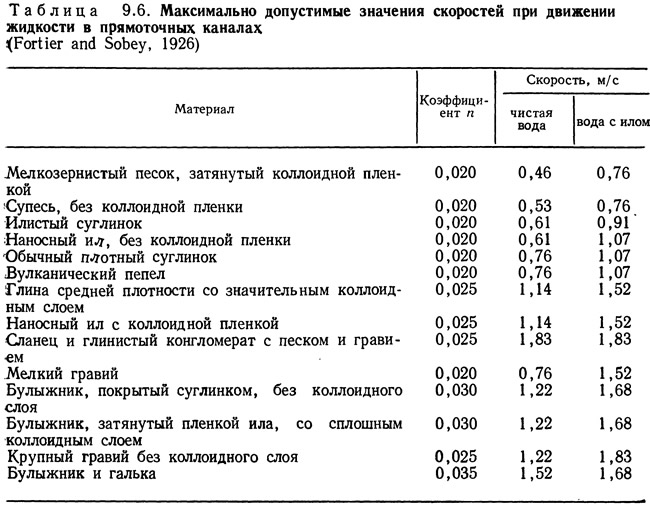
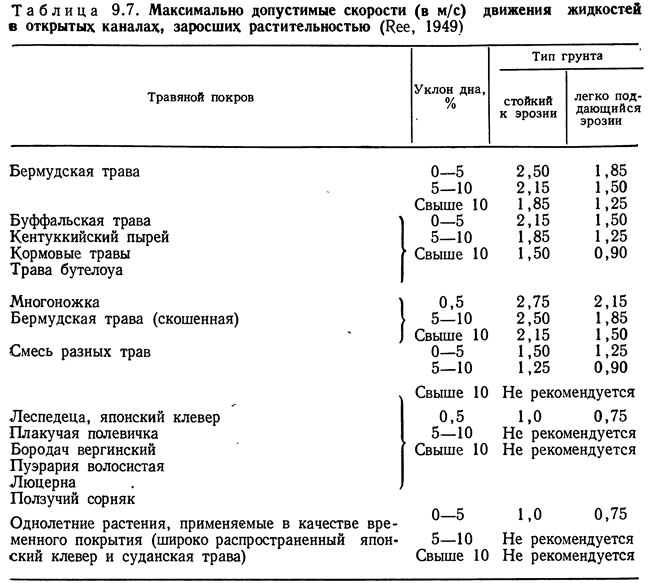
Большинство открытых каналов рассчитывается по формуле Маннинга и уравнению неразрывности. Среди них—открытые каналы, реки, ручьи, дренажные канавы, лотки и сточные желоба. При расчете земляных каналов или каналов, покрытых растительностью, необходимо учитывать ограничения влияния эрозии и толщины осадков (дополнительно к ограничениям, накладываемым формулой Маннинга и местным рельефом). Скорости, превышающие допустимые значения, вызывают эрозию стен каналов, а низкие скорости ускоряют рост отложений; последнее может вызвать необходимость увеличения поперечного сечения канала, что приводит к значительному возрастанию капитальных затрат. В табл. 9.6 и 9.7 приведены максимально допустимые значения скоростей для различных грунтов и отложений. Минимально допустимая скорость движения жидкости в канале определяется условием возможного образования отложений из материалов взвешенных в жидкости. Желательно, чтобы скорости превышали минимально допустимые значения, так как сооружение каналов с низкой скоростью движения воды обходится очень дорого.
Форма поперечного сечения канала определяется его назначением, видом материала, из которого выполнены дно и стенки, экономическими соображениями, а также из условия минимальных потерь жидкости на испарение. Каналы с бетонированными стенками или подобные им обычно имеют прямоугольную и трапецеидальную формы поперечного сечения. Каналы, прокладываемые в грунте, обычно делают трапецеидальной формы, так как при прямоугольной форме сечения боковые стенки таких каналов неустойчивы. Боковые стенки каналов с трапецеидальной формой сечения могут иметь различный уклон — от 3:1 (отношение горизонтального катета к вертикальному) до 1:1; последняя величина встречается лишь в условиях исключительно плотного грунта. Желоба для транспортировки рыбы или овощей часто имеют сечение прямоугольной формы, что объясняется конструктивными и экономическими соображениями. Глубокие узкие каналы позволяют значительно уменьшить площадь зеркала воды и сократить таким образом потери на испарение.
С точки зрения гидравлики форму поперечного сечения канала следует выбирать с таким расчетом, чтобы при минимальном смоченном периметре площадь живого сечения потока была максимальной, т. е. гидравлический радиус должен быть максимальным. Чем больше гидравлический радиус, тем меньше сопротивление преодолеваемое потоком, и тем больше расход воды при одинаковом поперечном сечении. В этом смысле наиболее совершенной является форма круга, так как у него максимальный радиус R. Однако для каналов больших размеров круглое сечение не применяется, так как это слишком сложно и дорого.
Уравнение (9.50) характеризует зависимость между шириной канала по дну и и глубиной h для наиболее выгодного с точки зрения гидравлики сечения при прямоугольной форме канала:
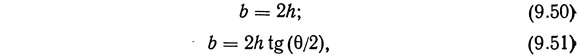
где θ — угол между боковой стенкой канала и горизонтальной плоскостью.
Облицовка внутренней поверхности открытых каналов имеет несколько преимуществ. Бетонирование, например, значительно сокращает утечки воды, максимально допустимые скорости, могут быть увеличены. За счет увеличения скоростей появляется возможность пропустить требуемый расход через меньшее поперечное сечение. При сооружении каналов малого сечения уменьшается стоимость постройки. Если экономия за счет уменьшения поперечного сечения канала с избытком компенсирует затраты на его облицовку, то облицовка становится экономически выгодной. Однако увеличение скоростей не всегда возможно, для этого необходим соответствующий уклон дна. Обслуживание облицованных каналов обходится дешевле, так как на внутренних стенках таких каналов не развивается растительность.
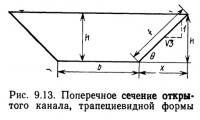
Пример 9.8. Определить размеры открытого канала трапециевидного сечения (рис. 9.13), по которому должна подводиться вода (1,5 м3/с) из реки к форелевому хозяйству. Канал прокладывается в плотном глинистом грунте, без облицовки. Уклон боковых стенок принять равным √
По табл. 9.6 максимально допустимая скорость равна 1,14 м/с, коэффициент шероховатости n=0,025. Если предположить, что скорость в канале равна максимально допустимой, то
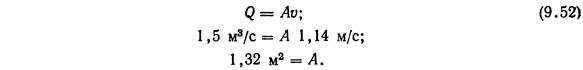
Таким образом, площадь поперечного сечения канала при скорости движения в нем 1,14 м/с и расходе 1,5 м3/с должна составлять 1,32 м2.
Площадь поперечного сечения канала рассчитывается по формуле
Из уравнения (9.13) и определения тангенса
Из подобия треугольников
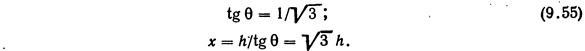
Подставив выражение (9.55) в формулу (9.53), получаем
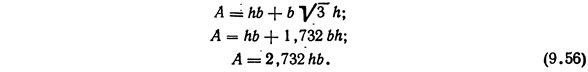
Поперечное сечение канала должно быть максимально выгодным с точки зрения гидравлики. Для трапециевидной формы, сечения зависимость ширины канала по дну b от глубины канала h и угла наклона боковых стенок к горизонтальной плоскости θ имеет следующий вид:
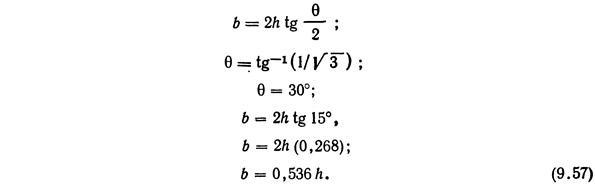
Последнее выражение позволяет исключить одну из неизвестных величин в формуле (9.56):
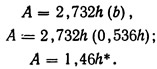
Выше [уравнение (9.52)] площадь поперечного сечения была определена в 1,32 м2. Таким образом,
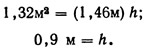
Ширину канала по дну можно подсчитать, воспользовавшись выражением (9.57):
Величины h, b и θ определяют поперечное сечение канала. Однако до сих пор не учитывался уклон дна канала и его влияние на скорость. Это ограничение учитывается расчетными величинами b и h и формулой Маннинга
Если значения n и S известны из условия задачи, то значение R следует определить
Площадь поперечного сечения была ранее определена в 1,32 м2. Длину смоченного периметра pw можно подсчитать из рис. 9.13, для b и h берутся полученные выше значения.
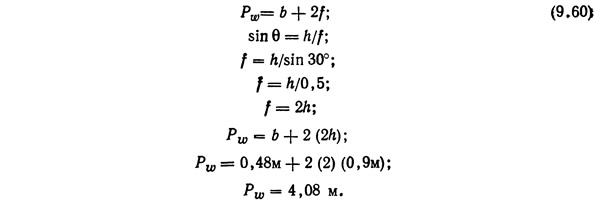
Отсюда
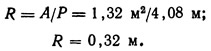
Подставляя в формулу (9.58), получим
(Уклон дна канала, заданный в процентах, переведен в десятичную величину).
Следовательно, скорость в канале равна 0,56 м/с, а не 1,14 м/с, как было принято. Действительный расход воды в канале составит
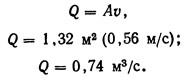
Однако в соответствии с проектным заданием расход должен равняться 1,5 м3/с. Поскольку уклон дна канала ограничен топографией местности, остается увеличивать поперечное сечение. Это можно выполнить различными способами, в нашем случае попробуем увеличить ширину канала по дну до 0,75 м.
Во всех случаях смоченный периметр должен быть минимальным, тогда условия, выраженные формулой (9.51), остаются в силе.

Поскольку уклон дна канала не изменился, выражение (9.56) может быть использовано для дальнейшего расчета.
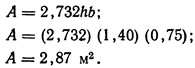
Смоченный периметр можно определить по формуле (9.61).

Отсюда
Теперь, сделав соответствующие подстановки, можно выполнить расчет по формуле Маннинга

Полученное значение расхода превышает заданное, равное 1,5 м3/с; следовательно, наиболее подходящая ширина канала должна находиться где-то между значениями 0,75 и 0,48, фигурировавшими в расчете в качестве предположительных. Следуя той же методике подбора,
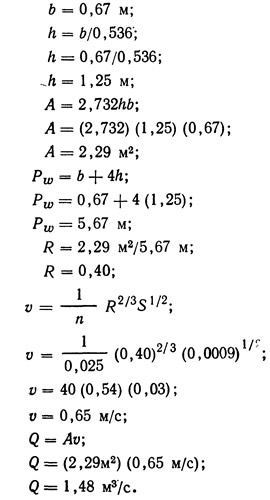
Поскольку значение 1,48 м3/с весьма близко к заданному 1,5 м3/с, на этом расчет можно прекратить и принять за окончательные следующие размеры поперечного сечения трапецеидального канала:
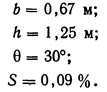
При расчете открытых каналов многие задачи решаются таким же, как в примере (9.8), методом последовательных приближений. Некоторые задачи можно решать непосредственно. Метод последовательных приближений отнимает много времени. Практический опыт работы помогает сократить количество промежуточных этапов решения такого рода задач. Кроме того, существует много справочников, в которых приводятся значения b, h и S. Такие справочники позволяют существенно сократить время, затрачиваемое на подсчеты.